Stealing finetuning data with corrupted models

A colleague (thanks James!) mentioned an interesting paper – Privacy Backdoors: Stealing Data with Corrupted Pretrained Models by Shanglun Feng and Florian Tramèr at ETH Zurich. The paper describes a supply chain data stealing attack in which an adversary can corrupt a neural network model such that sensitive finetuning data can either be recovered or inferred and featured at ICML 2024. Note: I wrote most of this post in autumn 2024 but got sidetracked from publishing until now :)

I used GPT 4o to interactively extract details from the paper (partial transcript here) and then dived in manually to check important details and validate integrity. I also prompted/wrote a basic non-transformer version of this attack which you can access here.

tl;dr - don’t worry just yet, but check your pretrained model weights for relatively large values if you are concerned.

What is the Threat Model?

Let’s start with the overall picture of who and what is involved in this attack.

Ecosystem

There are two entities, an attacker and a target, an initial pretrained neural network model (just model henceforth), a corrupted model, and a finetuned model. The specific models discussed in the paper are multi-layer perceptron (MLPs) and transformer models, both of the image and text-based variety, but I will focus on text-based transformer models i.e., large language models (LLMs) in this post as I think they (1) offer a more intuitive understanding of the attack, and (2) likely represent the most valuable target for attackers. In other words, this attack impacts large language models (LLMs) as we will explore below.

The Attack Chain

I think the threat model is best explained via a high-level walkthrough of the attack chain, which is as follows:

1. The attacker starts with a pretrained model, most likely downloaded from Hugging Face, and will produce a corrupted model that will be provided to the target.

2. The target downloads the corrupted model and finetunes it using sensitive data, presumably for improved performance in a downstream task. The target makes the finetuned model accessible, either wholly (e.g., by reuploading it to Hugging Face or because it is stolen) or by query (e.g., through an application accessible to the attacker).

3. Finally, the attacker learns sensitive information either recovering entire input sequences, or inferring particular data was used by the target during finetuning, depending on whether the model was available wholly or only by query, respectively.

Threat Model Assumptions

For the attack chain to succeed and be worthwhile (i.e., rational) there are some assumptions to consider carefully. Here’s the ones I can think of and whether they seem likely or not.

The target will choose the attacker’s corrupted model as its starting point for developing their application. On the one hand there is a strong incentive to use pretrained models owing to the cost of training modern LLMs from scratch. For example, ChatGPT 4 is estimated to have cost more than $100 million to train. However, I think this is a strong assumption if you consider the incentives for selecting a pretrained model during development. If the incentive is largely performance, then proprietary models direct from OpenAI, Google, Meta, etc dominate evaluation leaderboards such as LMSYS Chatbot Arena. Worsening the odds for our would-be attacker, the results (see Appendix D2 in the paper) show that corrupted transformer models may perform significantly worse (e.g., 12-27% reduction in accuracy) than their pretrained counterparts. The exact reduction in performance depends on the specific data traps inserted in the corrupted model, and on the target’s task, but is essentially unavoidable since propagating error losses are used to trap data. Still, maybe there are some applications where attackers could slip into the supply chain such as non-english models or smaller models for edge devices. – unlikely.

The corrupted model will be finetuned using stochastic gradient descent (SGD) i.e., not using Adam or low-rank adaptation (LoRA) for multiple epochs. This is mentioned explicitly in the Threat Model section of the paper. This seems unlikely as variants of SGD, such as Adam, and LoRA are typically used for LLM finetuning. Incentives diminishing the attacker’s odds include the target likely being very concerned about cost, compute resources, and time. Adam is usually preferable to SGD because of more effective and efficient convergence, and greater robustness to choice of hyperparameters. Similarly, LoRA requires less memory, trains faster, and is more likely to preserve the original model’s capabilities compared to full-parameter finetuning [1].

Figure 1: Backdooring a linear unit h via hidden unit h′ connected to the model's logit layer z.

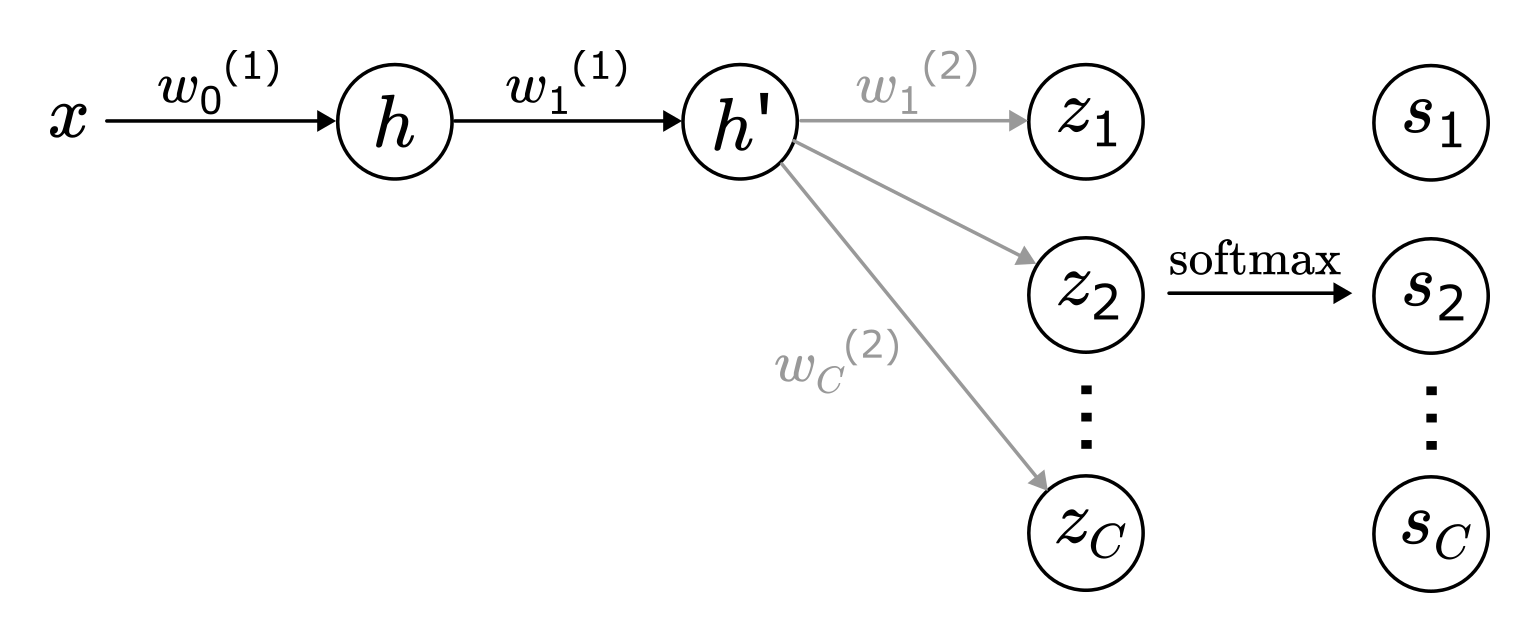
Concerning the SGD assumption, this attack method depends on setting the weights and biases of target neurons such that sensitive data is trapped after a gradient update. This is made possible by “shutting down” neurons after one update in which the input is encoded in the neuron weights. This critically relies upon a large positive gradient being applied during the optimisation step. e.g., let \(\eta\) denote the learning rate. Then for the backdoor unit \(h\) as shown in Figure 1, on a new input \(x\): \begin{equation} {w_1^{(1)}}’ = w_1^{(1)} - \eta \nabla_{w_1^{(1)}} \mathcal{L} = w_1^{(1)} - \eta \left( \frac{\partial \mathcal{L}}{\partial h} \cdot x \right) \end{equation} Where the gradient is computed as follows: \begin{equation} \frac{\partial \mathcal{L}}{\partial h} = \frac{\partial \mathcal{L}}{\partial h’} \cdot \frac{\partial h’}{\partial h} = \left( \sum_{i=1}^{C} (s_i - y_i) \cdot w_i^{(2)} \right) \cdot w_1^{(1)} \end{equation} Thus, when the target is using SGD to optimise an MLP classifier, the attacker can cause the gradient \(\frac{\partial \mathcal{L}}{\partial h}\) to be large by setting \(w_1^{(1)}\) to be large (with probability \(1-\frac{1}{C}\) where \(C\) is the number of classes). Note that \(w_1^{(2)},\ldots,w_C^{(2)}\) are randomly initialised before finetuning because they correspond to the original pretraining classification task, so are not assumed to be controlled by the attacker.

In contrast to SGD, Adam is designed specifically to reduce high variance and oscillations in gradient updates. This stabilises training and improves convergence, strongly motivating Adam optimisation in real-world models e.g., ChatGPT [2]. However, Adam’s refinements of SGD make the construction of successful data traps (corrupted neurons) substantially more challenging. In particular, the momentum and adaptive learning rates in Adam’s gradient update rule work against exploiting large gradient updates to trap data. – unlikely.

The attacker has sufficient knowledge of the target’s sensitive data. Data traps must be set up to activate highly when particular features, or text tokens, are present in the finetuning data. A further challenge in transformer models is to capture a complete input rather than individual tokens from different inputs. To achieve this, the authors design “keyed” backdoors that activate only for tokens at a specific position in a single input sequence. The attacker therefore needs to know the positions of tokens in sequences likely to contain sensitive data in the target’s dataset. Furthermore, the attacker needs to understand the overall finetuning dataset well enough to target sequences that occur infrequently. This second requirement arises because activating data traps frequently frustrates the recovery of sensitive tokens and has a greater impact on model performance. – somewhat unlikely.

From SGD to Adam

Reading the paper left me wondering how feasible would it be to extend the attacks to target Adam optimisation?

Let the gradient of the loss function at step \(t\) be defined \(g = \nabla_{w_1^{(1)}} \mathcal{L}\), then where \(\beta_1,\beta_2 \in [0,1]\) parameterise exponential decay weights, Adam maintains: \begin{equation} m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t \end{equation} \begin{equation} v_t = \beta_1 v_{t-1} + (1-\beta_1)g_t^2 \end{equation} which denote first (eqn. 3) and second (eqn. 4) moment vectors, which estimate the mean and uncentered variance of the loss gradient, respectively.

The moment estimates are initialised to \(0\), so bias-correction is applied: \begin{equation} \hat{m}_t = \frac{m_t}{1 - \beta_1^t} \end{equation} \begin{equation} \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t} \end{equation}

Finally, where \(\epsilon\) is small constant (e.g., \(10^{-8}\)) added for numerical stability, the model weights are updated (cf. eqn. 1) as follows: \begin{equation} w_{t+1} = w_{t} - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} \end{equation}

Recall the attacker uses large loss gradients to switch off corrupted data trap neurons and prevent further updates from erasing trapped data. In Adam however, both momentum and bias-correction stymie large gradients.

To illustrate the challenge I created an MLP data trap implementation for further research. Prompting an implementation of this attack required a lot of fiddling and… gasp - even writing code in places, but I suspect it was still a net win. You can find the code here if you want to have a look for yourself.

The implementation builds a basic MLP model for the MNIST handwritten digit classification task. Inputs are handwritten digits, 28x28 pixel images flattened to a vector of 784, and the output is the probability of each possible digit 0-9. There is just one hidden layer of size 256. Pseudocode is as follows:

1. Load MNIST dataset and split into training (90%) and finetuning (10%) subsets.

2. Train the MLP using SGD and the training dataset.

3. Corrupt the pretrained model by setting a large weight in the hidden layer.

4. Finetune the corrupted model using SGD and, separately for comparison, Adam.

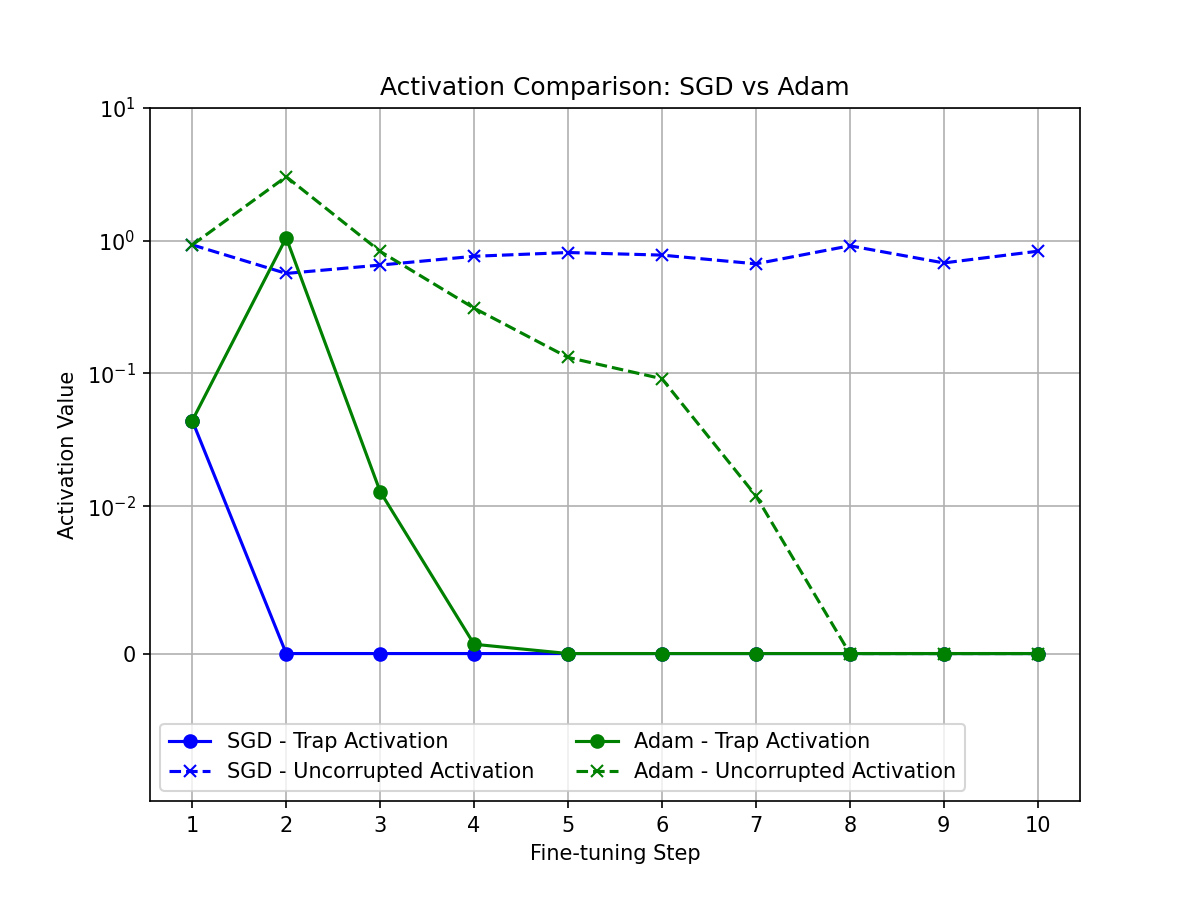
As shown in Figure 2 below, I keep track of the activations, gradients, and weights during the initial finetuning steps. The results illustrate how SGD optimisation is exploited to trap data and how the attack is diminished by Adam. The attack begins in the first step as infrequent finetuning data is not targeted. To begin with the data trap neuron is highly activated irrespective of the optimisation method.

(a)

(b)

(c)

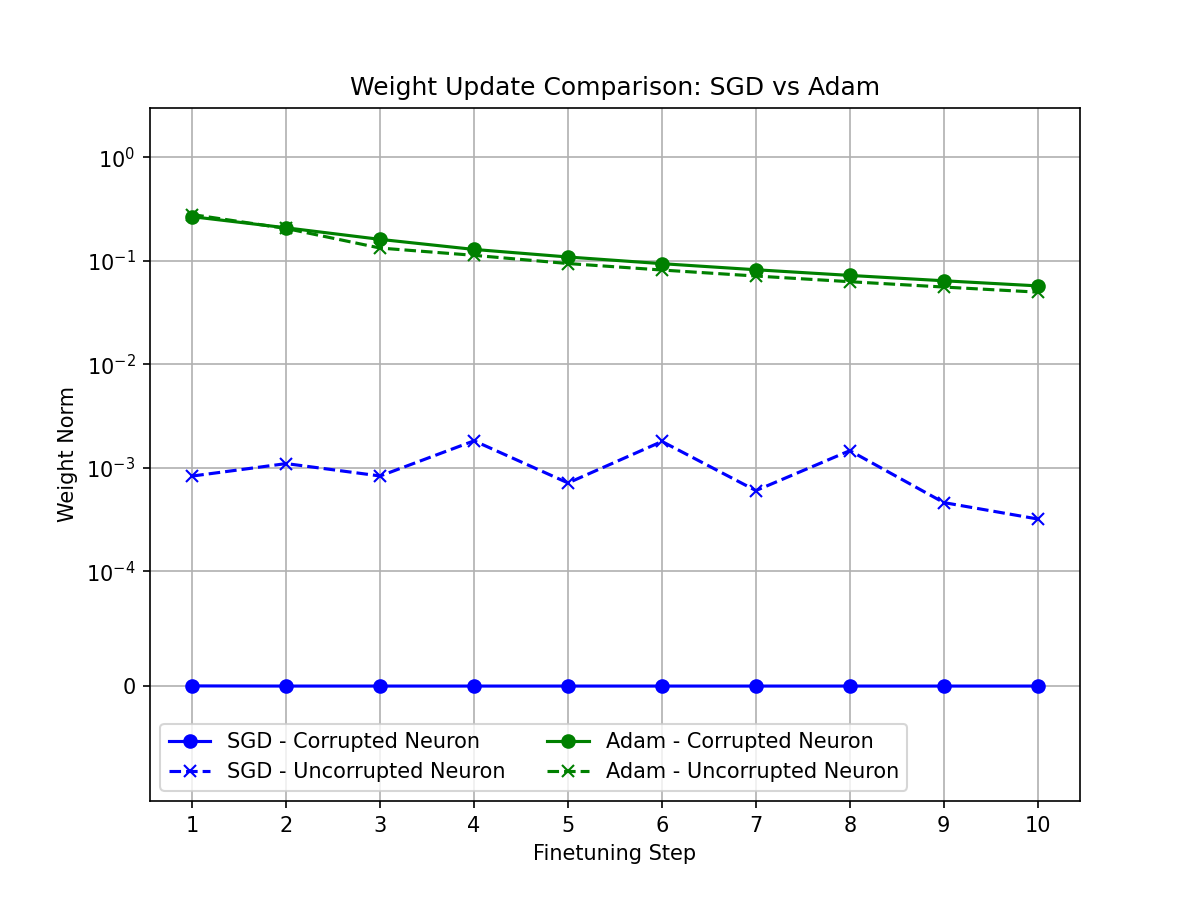
Figure 2(a) shows how the corrupted neuron (SGD) is highly activated (\(e^-2\)) in the first step and then “switched off” for the remainder. Neuron corruption reduces activation over time compared with controls, but the momentum of Adam prevents the complete and sudden neuron “shut down” required to effectively trap data.

Figure 2(b) shows that corrupted neurons experience highly dampened gradients compared to uncorrupted neurons. Although not visible on the plot owing to scaling, the corrupted neuron under SGD sees a loss gradient only in the first step (\(e^-7\)) and is \(0\) thereafter. Under Adam optimisation, the gradient varies much more until step 5 and then also remains \(0\). Maintaining a loss gradient of 0 is essential to ensure data is trapped once and then remains without addition until the end of finetuning.

Finally, Figure 2(c) clearly demonstrates the effectiveness of the data trap method only when SGD optimisation is used. Despite similar corrupted neuron activation in the first step, Adam’s momentum smooths out the weight updates–averaging the result over many steps rather than trapping specific data.

At the end of finetuning in the example above the trapped pixel value is recovered precisely from the SGD finetuned model. The value is also approximately recovered from the Adam finetuned model.

Final Thoughts

There are lots of additional challenges that make stealing finetuning data from transformer models even more difficult detailed in the paper. Overall I think this is very interesting and thorough work, but I’m not convinced it will be seen in practice without further refinement and some seemingly unlikely circumstances favouring SGD optimisation of a corrupted model.

If you’re concerned about this attack, or a future evolution of it, then you should consider the threat model assumptions and try to ensure they are made as unlikely as possible. The main mitigation is to avoid finetuning corrupted models which can probably be accomplished by using models from trusted sources and validating the model weights. In practice, you can likely just check for particularly large weights (e.g., 1-2 orders larger than the median) as these are required to trap data effectively. Following this, you should also evaluate the pretrained model to check for expected performance w.r.t public benchmarks before applying your data.

It is worth knowing that SGD is inherently more susceptible to this type of attack should you have any reason to be using it (i.e., [4]). Differentially Private SGD (DP-SGD) [3] is another technique that mitigates data leakage during model training, essentially by adding noise to the loss gradients of each optimisation step. This paper provides a strong attacker which, despite only observing the final finetuned model, allows DP-SGD privacy attacks that reach the upper bound on information leakage. If you’re using DP-SGD and need to mitigate this attack, then you should adopt conservative privacy budgets accounting for an upper-bound adversary.

Bibliography

1. Edward J. Hu et al. (2021). LoRA: Low-Rank Adaptation of Large Language Models. arXiv:2106.09685. (Online)
2. Tom B. Brown et al. (2020). Language Models are Few-Shot Learners. NeurIPS 2020. (Online)
3. Milad Nasr et al. (2021). Adversary Instantiation: Lower Bounds for Differentially Private Machine Learning. IEEE S&P 2021. (Online)
4. (Kumar A. et al. (2023). How to Fine-Tune Vision Models with SGD. (Online)